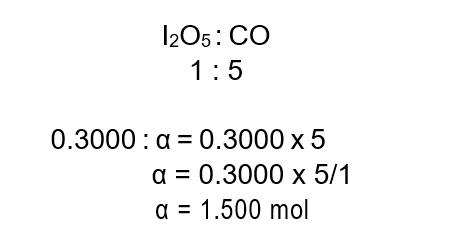Curriculum
Stoichiometric Relationship
INTRODUCTION TO THE PARTICULAR NATURE OF MATTER AND CHEMICAL CHANGE
0/2ASSIGNMENTS
0/2MOLE CONCEPT
0/2ASSIGNMENTS
0/2REACTING MASSES AND VOLUMES
0/2ASSIGNMENTS
0/2Limiting Reagents, Theoretical and Experimental Yields, Volumetric Analysis
Working Method : how to balance chemical equations
The examples below involve reactions of metals. Metals are below and to the left of the metalloids in the periodic table.
Remember that to balance an equation you change the coefficient of a formula (add a number in front of the formula). You do not change the formula itself.
Step 1 : First balance the metallic element on each side of the equation – add a number in front of the symbol on one side if necessary, so that there is the same number of atoms of this element on each side.
Step 2 : Balance any elements that occur in only one formula on the reactant and products side. Sometimes polyatomic ions remain unchanged in reactions and they can be balanced easily at this stage.
Step 3 : Balance the remaining elements if necessary.
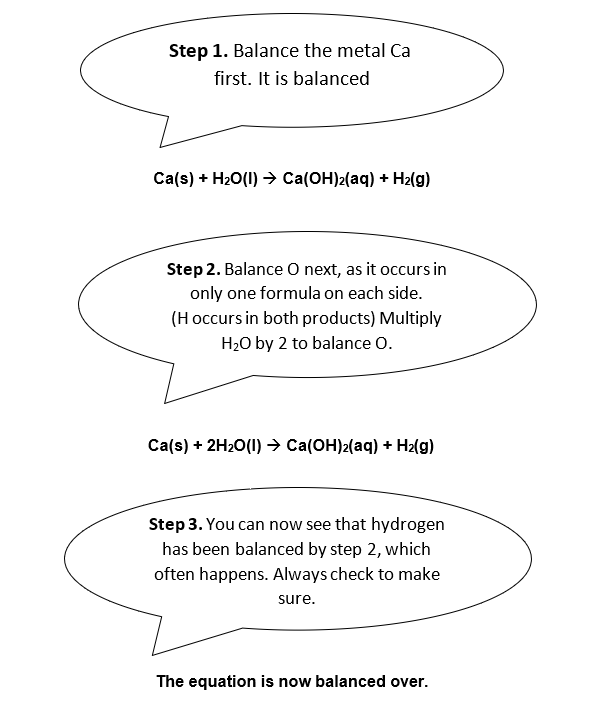
Example 1
The alkaline earth metal calcium reacts with water to produce an alkaline solution. Balance the following equation.
Example 2
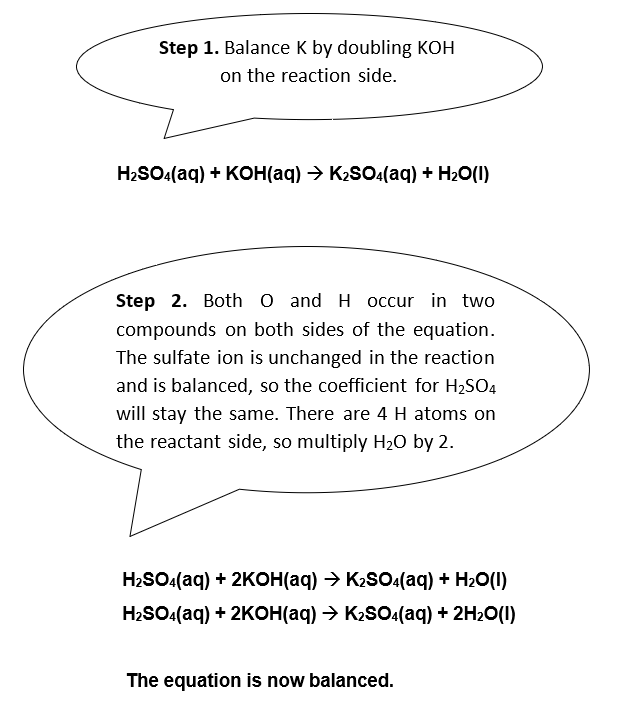
Potassium hydroxide is a soluble base that can neutralize the diprotic acid sulfuric acid. Diprotic acids produce two hydrogen ions when they dissociate. Balance the following equation.
Some types of reaction
Combination or synthesis reactions involve the combination of two or more substances to produce a single product :
C(s) + O2(g) → CO2(g)
Decomposition reactions involve a single reactant being broken down into two or more products :
CaCO3(s) → CaO(s) + CO₂(g)
Single replacement reactions occur when one element replaces another in a compound. An example of this type of reaction is a redox reaction :
Mg(s) + 2HCl(aq) → MgCl2(aq) + H₂(g)
Double replacement reactions occur between ions in solution to form insoluble substances and weak or non-electrolytes, also termed metathesis reactions:
HCI(aq) + NaOH(aq) → NaCl(aq) + H₂O(l)
The atom economy
The global demand for goods and services along with an increasing world population, rapidly developing economies, increasing levels of pollution, and dwindling finite resources have led to a heightened awareness of the need to conserve resources. Synthetic reactions and industrial processes must be increasingly efficient to preserve raw materials and produce fewer and less toxic emissions. Sustainable development is the way of the future.
To this end the atom economy was developed by Professor Barry Trost of Stanford University Stanford, CA, USA. This looks at the level of efficiency of chemical reactions by comparing the molecular mass of atoms in the reactants with the molecular mass of useful compounds.
The atom economy is important in the discussion of Green Chemistry, which we will discuss later in this book. In an ideal chemical process the amount of reactants = amounts of products produced. So, an atom economy of 100% would suggest that no atoms are wasted.
Illustration : The concept of the atom economy gives the measure of the unwanted product produced in a particular reaction.
For example : Conversion of Butan-1-ol to 1-bromobutane
CH3CH2CH2CH2OH + NaBr + H2SO4 → CH3CH2CH2CH2Br + NaHSO4 + H2O
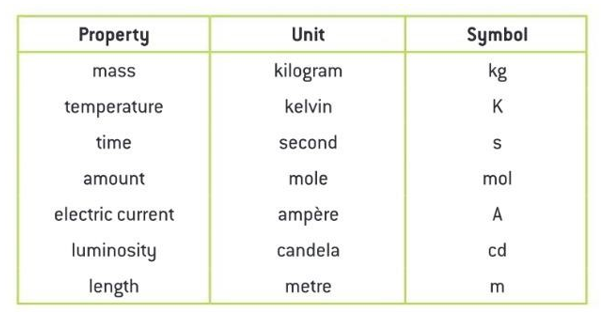
What is the SI Unit?
SI unit is an international system of measurements that are used universally in technical and scientific research to avoid the confusion with the units. Having a standard unit system is important because it helps the entire world to understand the measurements in one set of unit systems. Following is the table with base SI units :
Stoichiometry
A balanced chemical equation provides information about what the reactants and products are, their chemical symbols, their state of matter, and also the relative amounts of reactants and products. Chemical equations may also include specific quantitative data on the enthalpy of the reaction. Stoichiometry is the quantitative method of examining the relative amounts of reactants and products. An understanding of this is vital in industrial processes where the efficiency of chemical reactions, particularly the percentage yield, is directly linked to the success and profitability of the organization.
From a balanced chemical equation the coefficients can be interpreted as the ratio of the amount, in mol, of reactants and products. This is the equation for the reaction used for the manufacture of ammonia in the Haber process :
N₂(g) + 3H2(g) = 2NH3(g) ΔΗ = -92.22 kJ
It shows that one molecule of nitrogen gas and three molecules of hydrogen gas combine in an exothermic reaction to produce two molecules of ammonia. However, when setting up a reaction the reactants may not always be mixed in this ratio – their amounts may vary from the exact stoichiometric amounts shown in the balanced chemical equation.
Stoichiometry helps us determine how much substances is needed or is present. Things that can be measured are,
1. Reactants and products mass
2. Molecular weight
3. Chemical equation
4. Formulas
In simple words, Stoichiometry as the calculation of products and reactants in a chemical reaction. It is basically concerned with numbers.
Stoichiometry is an important concept in Chemistry that helps us use balanced chemical equations to calculate amounts of reactants and products. Here, we make use of ratios from the balanced equation. In general, all the reactions that take place are dependent on one main factor, that is, how much substance is present.
Stoichiometric Coefficient
The stoichiometric coefficient or stoichiometric number is the number of molecules that participate in the reaction. If you look at any balanced reaction, you can notice that there are an equal number of elements on both sides of the equation. The stoichiometric coefficient is basically the number present in front of atoms, molecules or ions.
Stoichiometric coefficients can be fractions as well as whole numbers. In essence, the coefficients help us to establish the mole ratio between reactants and products.
Balanced Reactions and Mole Ratios
Atoms and molecules are extremely small in size, and their numbers in a very small amount of a substance are very large. Therefore, to represent atoms and molecules in bulk, a mole concept was introduced. One mole of any substance contains 6.022 x 1023 numbers of that substance. This number is also known as Avogadro’s number.
The mass of one mole of a substance in grams is called molar mass.
The molar mass of one mole of a substance is numerically equal to the atomic / molecular formula mass.
Let us take one example of a balanced chemical equation,
3Fe(s) + 4H2O(l) → Fe3O4(s) + 4H2(g)
The quantitative information drawn from this balanced chemical equation is
1. 3 mole of Fe reacts with 4 moles of H2O to yield one mole of Fe3O4 and 4 moles of H2.
2. 168g (56×3) of Fe reacts with 72g(18×4) of H2O to yield 231g of Fe3O4 and 8g of H2 gas.
If the reactants and products are in gaseous form, then the molar volume is taken into consideration. One mole of any gas occupies 22.4 litres.
The limiting reagent
Experimental designers of industrial processes use the concept of a limiting reagent as a means of controlling the amount of products obtained. The limiting reagent, often the more expensive reactant, will be completely consumed during the reaction. The remaining reactants are present in amounts that exceed those required to react with the limiting reagent. They are said to be in excess.
It is the limiting reagent that determines the amount of products formed. Using measured, calculated amounts of the limiting reagent enables specific amounts of the products to be obtained. The assumption made here is that the experimental or actual yield of products achieved is identical to the theoretical or predicted yield of products. This is rarely the case. Much effort is focused on improving the yield of industrial processes, as this equates to increased profits and efficient use of raw materials.
In a chemical reaction, it is possible that one of the reactants is present in excess amount. Some of these excess reactants will, therefore, be left over when the reaction is complete; the reaction stops immediately as soon as one of the reactants is totally consumed.
The substance that is totally consumed in a reaction is called the limiting reagent.
Let us take one example of a chemical reaction to understand the limiting reagent concept.
N2 + 3H à 2NH3
Suppose we have one mole of N2 reacting with one mole of H2. But from the balanced chemical equation, one mole of N2 requires three moles of H2. So, the limiting reagent in this reaction is H2.
How to find Limiting Reagent?
The determination of the limiting reactant is typically just a piece of a larger puzzle. In most limiting reactant stoichiometry problems, the real goal is to determine how much product could be formed from a particular reactant mixture. The limiting reactant or reagent can be determined by two methods.
1. Using the mole ratio
2. Using the product approach
In order to calculate the mass of the product first, write the balanced equation and find out which reagent is in excess. Using the limiting reagent calculate the mass of the product.
The following points should be considered while attempting to identify the limiting reagent :
· When there are only two reactants, write the balanced chemical equation and check the amount of reactant B required to react with reactant A. When the amount of reactant B is greater, reactant A is the limiting reagent.
· The reactant which is in a lesser amount than is required by stoichiometry is the limiting reactant.
· In an alternate method of finding the limiting reagent, the amount of product formed by each reactant is calculated.
· The limiting reactant is the reactant from which the minimum amount of product is formed.
· Also, if we calculate the amount of one reactant needed to react with another reactant, then the reactant which is in shortage would be the required limiting reactant.
Thus, the required limiting reagent for the reaction can be identified using the points provided above. These reagents are very important while calculating the percentage yield of a given reaction.
Limiting Reagent Examples
Consider 1 mol of oxygen and 1 mol of hydrogen are present to undergo the following reaction.
2H2 + O2 → 2H2O
Since the reaction uses up hydrogen twice as fast as oxygen, the limiting reactant would be hydrogen.
Example : 100g of hydrochloric acid is added to 100g of zinc. Find the volume of hydrogen gas evolved under standard laboratory conditions.
Solution :
The chemical equation for these reactions is given below.
2HCl(aq) + Zn(s) → ZnCl2(aq) + H2(g)
Zinc chloride is formed in excess so the limiting reagent here is hydrochloric acid.
73g of HCI = 22.41 of H2
100g of HCI = YL of H2
Y/ 22.4 = 100/73
Y = (100 x 22.4) / 73 Y = 30.6L
Therefore, 33.6L of H2 is produced under standard laboratory conditions.
Theoretical and experimental yields
The balanced chemical equation represents what is theoretically possible when a reaction is carried out under ideal conditions. It allows the expected amount of products to be calculated – the theoretical yield.
Scientists in industry work to maximize the yield of reactions and maximize profits. However, under experimental conditions and especially in large-scale processes, many factors result in a reduced yield of products. These factors could include :
· loss of products from reaction vessels
· impurity of reactants
· changes in reaction conditions, such as temperature and pressure
· reverse reactions consuming products in equilibrium systems
· the existence of side-reactions due to the presence of impurities.
To calculate the percentage yield a comparison is made between the theoretical yield and the actual amount produced in the process – the experimental yield :

Worked example : determining theoretical yield
Respirators are being used increasingly with concern for workplace safety and rising levels of environmental pollution. Iodine (V) oxide, I2O5 reacts with carbon monoxide, CO and can be used to remove this poisonous gas from air :
I2O5 (s) + 5CO(g) à I2(g) + 5CO2 (g)
100.0 g of I2O5 reacts with 33.6 g of CO. Calculate the theoretical yield of carbon dioxide and given an experimental yield, in mol, of 0.900 mol CO calculate the percentage yield.
Solution :
Step 1 : Calculate the initial amount in mol of reactants and determine the limiting reagent :
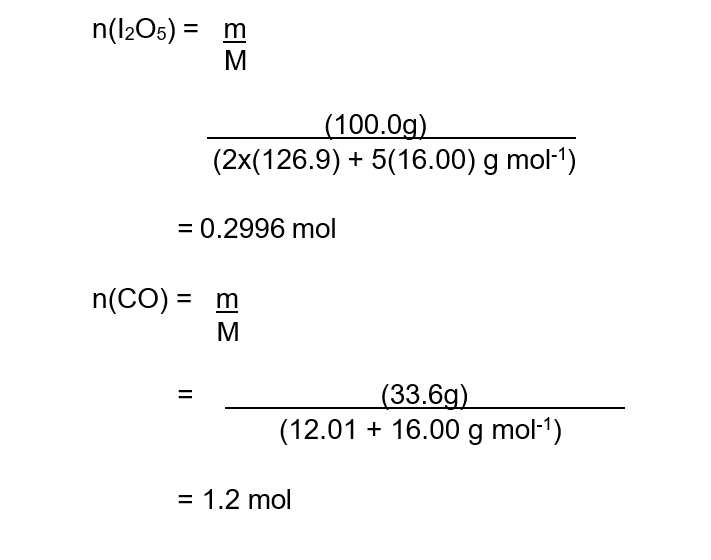
Step 2 : Using mole ratios, determine the limiting reagent.
The reaction of 0.3000 mol of I2O5 requires 1.50 mol of CO for completion. However, only 1.20 mol of CO is available; therefore, this is the limiting reagent.
The ratio of limiting reagent CO to product CO2 is 5:5 or 1:1. The number of mol of CO2 that is theoretically possible is therefore 1.2 mol.
It was found that 0.90 mol or 39.61 g of CO2 was produced. This is the experimental yield.
To determine the percentage yield of CO2 we first need to calculate the theoretical yield of CO2 :
m = M x n
= [12.01 + 2(16.00)] gmol-1 x 1.2 mol
= 52.8 g
Then :

Concentration
In a typical laboratory the majority of reactions carried out are in solution rather than in the gaseous phase. Chemists need to make up solutions of known concentrations.
A solution is a homogenous mixture of a solute that has been dissolved in a solvent. The solute is usually a solid, but could be a liquid or gas. When the solvent is water the solution is described as an aqueous solution.
The molar concentration of a solution is defined as the amount (in mol) of a substance dissolved in 1 dm³ of solvent. 1 dm³ = 1 liter (1 L).

Units of concentration
Units of concentration include :
· mass per unit volume, g/dm³
· mol per unit volume, mol/dm³
· parts per million (ppm) : one part in 1 × 106 parts. 1 ppm = 1 mg dm-3
Worked Examples : Concentration Calculation
Example 1 : Molarity of Solution
Calculate the concentration, using the unit mol dm-3, of a solution formed when 0.475 g of magnesium chloride, MgCl2 is completely dissolved in water to make a solution with a volume of 100 cm3.
Solution :

Example 1 : Concentration of ions
Determine the concentration, in mol dm-3 of the chloride ions in examples 1 above.
Solution :
When Solid MgCl2 is dissolved in water, the constitution ions are liberated :
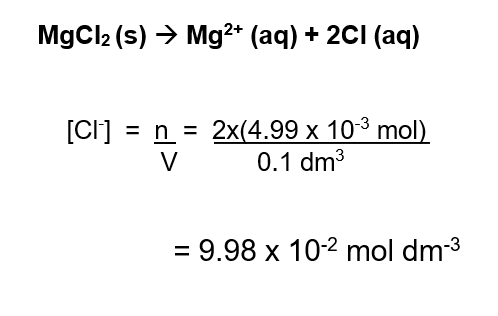
Example 1 : Mass of Solute
Calculate the mass, in g, of potassium hydrogen phthalate, C8H5O4K
(a primary standard) in 250 cm3 of a 1.25 mol dm-3 solution.
Solution :
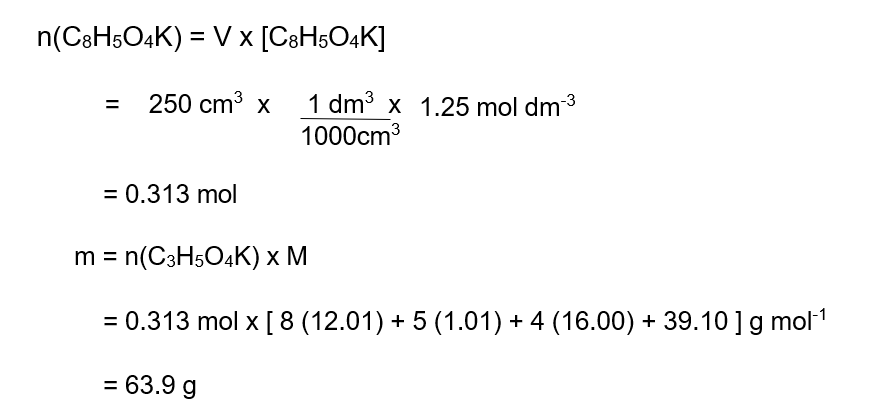
Example 1 : Concentration of Standard Solution
A standard solution is prepared by dissolving 5.30 g of sodium carbonate, Na2CO3 in 250 cm³ of distilled water in a volumetric flask. A 10.0 cm³ sample of this solution is removed by bulb pipette and diluted with water to the final volume of 0.100 dm³. Calculate the concentration, in mol dm³, of the diluted solution.
Solution :

Volumetric Analysis
The volumetric analysis involves the quantitative measurement of substance in terms of volume.
Principle: In volumetric analysis, a known volume (V₁) of the substance, whose concentration (N₁) is known, is reacted with the unknown volume (V2) of the solution of the substance, whose concentration (N2) is to be calculated. The volume V₁ is noted at the endpoint of the reaction. The concentration N2 is calculated using the following equation.
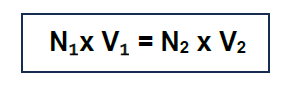
The endpoint of such a reaction is indicated by a change in colour or precipitation etc.
Terms involved in volumetric analysis are as follows :
1. Titration – The process of finding out the volume of solution required to react completely with the volume of another solution is called titration.
2. Titrant – The solution of known strength is called titrant.
3. Titrate – The solution whose concentration is to be estimated is called titrate.
4. Indicator – Indicators are reagents which change their colour when the reaction is complete.
Worked example : acid – alkali titration calculation
Example 1 : Calculate the volume, in dm3, of 0.390 mol dm-3 potassium hydroxide, KOH solution that will neutralize 25.0 cm3 of 0.350 mol dm-3 sulfuric acid, H2SO4.
2KOH(aq) + H2SO4(aq) à K2SO4(aq) + 2H2O(I)
Solution :
Step 1 : Calculate the amount, in mol, of H2SO4 : n(H2SO4) = CxV
= 0.350 mol dm-3 x 0.0250 dm3
= 8.75 x 10-3 mol
Step 2 : The mole ratio of acid : alkali is 1:2. Therefore 8.75 x 10-3 mol of acid reacts with 2(8.75 x 10-3 mol) = 1.75 x 10-2 mol of KOH.
Step 3 : Calculate the volume of KOH :
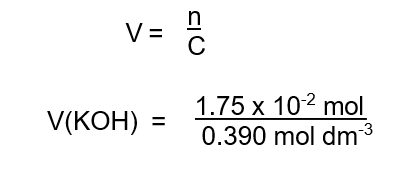
Stoichiometry Problems with Solutions
1. Calculate the mass of sodium hydroxide required to make 500 ml of 0.10 M solution.
Solution :
The molar mass of NaOH = 40g Volume of NaOH = 500ml = 0.5 L Molarity = 0.10M
Molarity = moles / volume in litres
= weight of NaOH = molarity x molar mass of NaOH x volume
= 0.10 x 40 x 0.5
= 2 g
2. How much volume of 11M HCI has to be diluted with water to prepare 3M of 400 ml HCI?
Solution :
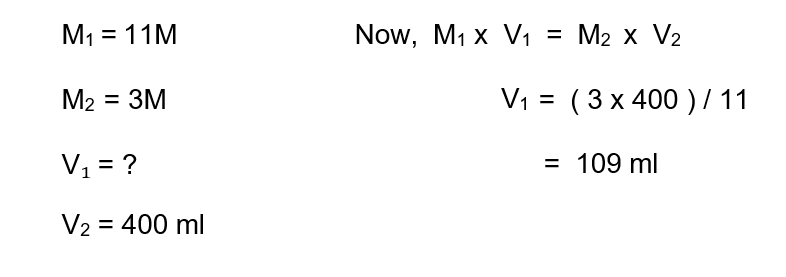
3. How many carbon atoms are present in 0.5 moles of oxalic acid (C2H2O4)?
Solution :
1 mole of oxalic acid = 6.022 x 1023 number of oxalic acid
0.5 mole of oxalic acid = 6.022 x 1023 x 0.5 number of oxalic acid Since there are 2 carbon per oxalic acid,
The number of carbon atoms in 0.5 moles of oxalic acid = 6.022 x 1023 x 0.5 x 2
= 6.022 x 1023
4. 0.5216g of a solid mixture containing Na2SO4 is dissolved in water and treated with an excess of BaCl2, resulting in the precipitation of 0.6168g What percentage of the mixture was BaSO4?
Solution :
Na2SO4 + BaCl2 → BaSO4 + 2NaCl
233g of BaSO4 is obtained from 142g of Na2SO4
So, 0.6168g of BaSO4 is obtained from = (142×0.6168) / 233
= 0.37g
Since the mass of the solid mixture is 0.5216 g,
The percentage of BaSO4 is solid mixture = (0.37/0.5216) x 100
= 70.34%
5. A solution containing 5 g of KOH and Ca(OH)2 is neutralized by an acid. If it consumes 0.1 g equivalents of the acid, calculate the composition of the solution.
Solution :
Let the mass of KOH present in mixture = x Mass of Ca(OH)2 = (5-x)g
Equivalent mass of KOH = 56; Equivalent mass of Ca(OH)2 = 37 Gram equivalent of KOH + Gram equivalent of Ca(OH)2 = Gram equivalent of acid
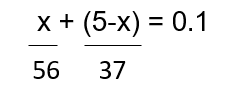
ð x = 3.83g
Mass of KOH in the sample = 3.83g Percentage of KOH = (3.83/5) x 100
= 76.6%
Percentage of Ca(OH)2 = (1.17/5) x100
= 23.4%
6. How many ml of 0.45 m HCl must be added to 25 ml of 1.00 m KOH to make neutral solution?
Solution :
1. Write balanced equation :
HCl + KOH à KCl + H2O
0.4m 9.00m
? ml 25ml
2. Find moles of known solution :
Here, KOH is the known solution.
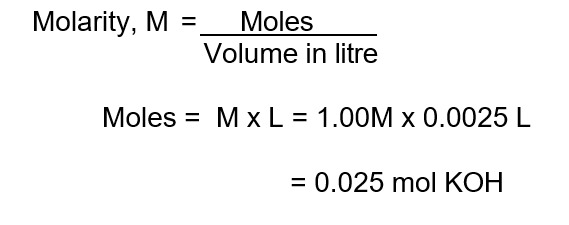
3. Use mole ratio to find moles of unknown solution :
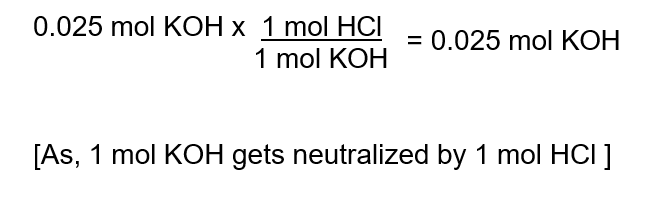
4. Solve the unknown solution :
Here, HCl is the unknown solution.

Therefore, 56 ml of 0.45m HCl will be needed to neutralize 25 ml of 1.00m KOH.
|
Step (H occurs in both products) Multiply H2O by 2 to balance O. |
|
Step 3. You can now |