Avogadro’s Law and Other Gas Laws

 

Boyle’s Law

 

Boyle’s law is a gas law which states that the pressure exerted by a gas (of a given mass, kept at a constant temperature) is inversely proportional to the volume occupied by it. In other words, the pressure and volume of a gas are inversely proportional to each other as long as the temperature and the quantity of gas are kept constant. Boyle’s law was put forward by the Anglo-Irish chemist Robert Boyle in the year 1662.

For a gas, the relationship between volume and pressure (at constant mass and temperature) can be expressed mathematically as follows.

P∝ (1/V)

Where P is the pressure exerted by the gas and V is the volume occupied by it. This proportionality can be converted into an equation by adding a constant, k.

P = k*(1/V) ⇒ PV = k

The pressure v/s volume curve for a fixed amount of gas kept at constant temperature is illustrated below.

 

                                  

 

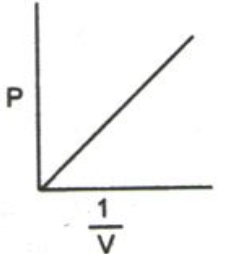
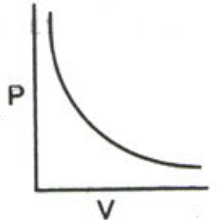
It can be observed that a straight line is obtained when the pressure exerted by the gas (P) is taken on the Y-axis and the inverse of the volume occupied by the gas (1/V) is taken on the X-axis.

Formula and Derivation

As per Boyle’s law, any change in the volume occupied by a gas (at constant quantity and temperature) will result in a change in the pressure exerted by it. In other words, the product of the initial pressure and the initial volume of a gas is equal to the product of its final pressure and final volume (at constant temperature and number of moles). This law can be expressed mathematically as follows: 

 

P₁V₁ = P₂V₂

 

Where,

• P₁ is the initial pressure exerted by the gas

• V₁ is the initial volume occupied by the gas

• P₂ is the final pressure exerted by the gas

• V₂ is the final volume occupied by the gas

 

This expression can be obtained from the pressure-volume relationship suggested by Boyle’s law. For a fixed amount of gas kept at a constant temperature, PV = k. Therefore,

 

P₁V₁ = k (initial pressure * initial volume)

 

P₂V₂ = k (final pressure * final volume)

 

\ P₁V₁ = P₂V₂

 

This equation can be used to predict the increase in the pressure exerted by a gas on the walls of its container when the volume of its container is decreased (and its quantity and absolute temperature remain unchanged).

Examples of Boyle’s Law

When a filled balloon is squeezed, the volume occupied by the air inside the balloon decreases. This is accompanied by an increase in the pressure exerted by the air on the balloon, as a consequence of Boyle’s law. As the balloon is squeezed further, the increasing pressure eventually pops it. An illustration describing the increase in pressure that accompanies a decrease in the volume of a gas is provided below.

 

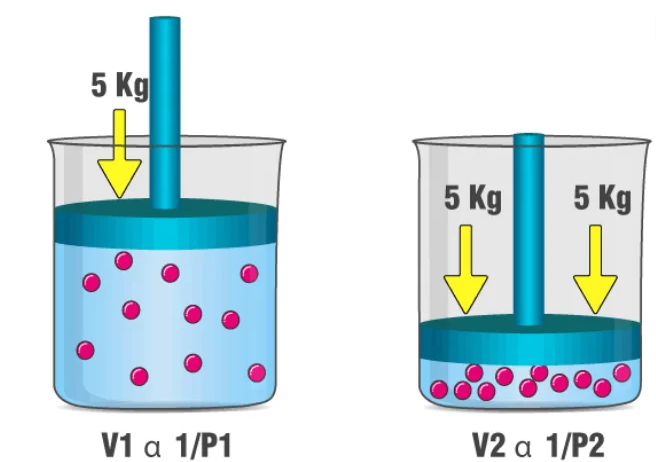
If a scuba diver rapidly ascends from a deep zone towards the surface of the water, the decrease in the pressure can cause the gas molecules in his/her body to expand. These gas bubbles can go on to cause damage to the diver’s organs and can also result in death. This expansion of the gas caused by the ascension of the scuba diver is another example of Boyle’s law. Another similar example can be observed in the deep-sea fish that die after reaching the surface of the water (due to the expansion of dissolved gasses in their blood).

 

 

Solved Exercises on Boyle’s Law

 

Exercise 1

A fixed amount of a gas occupies a volume of IL and exerts a pressure of 400 kPa on the walls of its container. What would be the pressure exerted by the gas if it is completely transferred into a new container having a volume of 3 liters (assuming the temperature and quantity of gas remains constant)?

 

Given,

 

Initial volume (V₁) = IL

Initial pressure (P₁) = 400kPd

Final volume (V₂) = 3L

As per Boyle’s law, P₁V₁ = P₂V₂ => (P₁V₁)/V₂

P₂ = (1L * 400 kPa) / 3L = 133.33 kPa

 

Therefore, the gas exerts a pressure of 133.33 kPa on the walls of the 3- liter container.

 

 

Exercise 2

 

A gas exerts a pressure of 3 kPa on the walls of container 1. When container 1 is emptied into a 10-liter container, the pressure exerted by the gas increases to 6 kPa. Find the volume of container 1. Assume that the temperature and quantity of the gas remain constant.

 

Given,

 

Initial pressure, P₁ = 3kPa

 

Final pressure, P₂ = 6kPa

 

Final volume, V₂ = 10L

 

According to Boyle’s law, V₁ = (P₂V₂) / P₁

 

V₁ = (6 kPa * 10 L) / 3 kPa = 20 L

 

Therefore, the volume of container 1 is 20 L.

 

 

Charle’s Law

 

 

Charles law states that the volume of an ideal gas is directly proportional to the absolute temperature at constant pressure. The law also states that the Kelvin temperature and the volume will be in direct proportion when the pressure exerted on a sample of a dry gas is held constant.

 

This law was formulated in the year 1780 by French physicist Jacques Charles. This law was described extensively in his unpublished work.

 

Charles’ law, also sometimes referred to as the law of volumes, gives a detailed account of how gas expands when the temperature is increased. Conversely, when there is a decrease in temperature, it will lead to a decrease in volume.

 

When we compare a substance under two different conditions, from the above statement, we can write this in the following manner :

 

 

 

 

V₂/V₁ = T₂/T₁

 Or

 

 V₁T₂ = V₂T₁

 

 

This above equation depicts that as absolute temperature increases, the volume of the gas also goes up in proportion.

 

In other words, Charle’s law is a special case of the ideal gas law. The law is applicable to the ideal gases that are held at constant pressure, but the temperature and volume keep changing.

 

  

Charles Law Everyday Examples

 

Here are some examples by which you can understand Charle’s law very easily.

 

In winter, as the temperature decreases, when you take a basketball outside on the ground, it shrinks. This is the only reason why it is important to check the pressure in the car tyres when you go outside during cold days. This is also the case with any inflated object and explains why it’s a good idea to check the pressure in your car tyres when the temperature drops.

 

If you overfill a tube that is placed in a pool on a hot day, it can swell up in the sun and burst. Similarly, as the turkey cooks, the gas inside the thermometer expands until it can “pop” the plunger. Pop-up turkey thermometers work based on Charles’ law. Another common application can be seen in the working of a car engine.

 

 

Charles Law Formula

 

Charle’s Law formula is written as,

 

V_I/T_I = V_F/T_F

 

Where,

 

 V_I = Initial volume

 

V_F = Final volume

 

T_I = Initial absolute temperature

 

T_F = Final absolute temperature

 

Here, we should remember that the temperatures are absolute temperatures that are measured in Kelvin, not in °F or °C.

 

 

Derivation of Charles Law

 

As we are aware of the fact that, at constant pressure, the volume of the fixed amount of the dry gas is directly proportional to absolute temperature, according to Charle’s law. We can represent the statement in the following manner :

 

 

 

V∝T

 

Since V and T vary directly, we can equate them by making use of the constant k.

 

V/T = constant = k

 

In this, the value of k depends on the pressure of the gas, the amount of the gas and also the unit of the volume.

 

V*T = k – – – (1)

 

Let us consider V₁ and T₁ to be the initial volume and the temperature, respectively, of an ideal gas.

 

Then, we can write equation (1) as

 

V₁/T₁ = k – – – (2)

 

After it lets change the temperature of the gas to T₂. Alternatively, if its

 

volume changes to V₂, then we can write,

 

V₂/T₂ = k – – – (3)

 

Equating the above equations, that is, equations 2 and 3, we get

 

 

 

V₁/T₁ = V₂/T₂

 Or

 

 V₁T₂ = V₂T₁

You may be unaware of the fact that, on heating up a fixed amount of gas, that is, by increasing the temperature, the volume also increases. Similarly, by lowering the temperature, the volume of the gas decreases. And at 0-degree centigrade, the volume of the gas also increases by 1/273 of its original volume for a unit-degree increase in temperature.

 

It is important to know, as already discussed above, that the unit of temperature must be in Kelvin, not in Celcius or Fahrenheit, to solve the problems related to Charle’s law. The temperature in Kelvin is also known as the absolute temperature scale. To convert the temperature in Celcius to Kelvin, you need to add 273 to the temperature in the Celsius scale.

 

According to Charle’s law, which states that the volume (V) of the gas is directly proportional to its temperature (T), that must be in Kelvin.

 

When the temperature changes one unit of the Kelvin scale, it equals to a change in one Celsius degree. Always remember that 0 on the Kelvin scale means -273 or “Absolute Zero”.

 

The density of the gas is inversely proportional to the temperature in the Kelvin when it is at a constant mass and pressure.

 

 

Graphical Representation of Charles Law

 

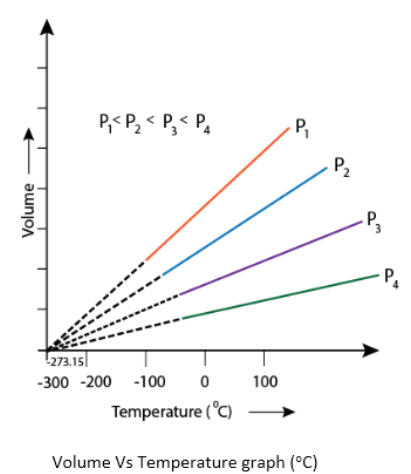
ISOBAR – The graph between V and T at constant pressure is known as isobar or isopiestics, and it always gives a straight line. A plot of V versus T (°C) at constant pressure is a straight line at – 273.15°C. This  -273.15°C  is the lowest possible temperature.

 

Charles Law Application in Real Life

This law has a wide application in daily life. Some are explained below.

·       In cold weather or in a cold environment, helium balloons shrink.

·       In winter, when the weather is cool, the capacity of the human lung decreases. This makes it more difficult for the athletes to perform on a freezing winter day, and it also makes it difficult for people to go jogging.

 

 

Charles Law Solved Problems

 

1.    A gas occupies a volume of 400 cm3 at 0^oC and 780 mm of Hg. How many litres of volume will the gas occupy at 80^oC and 780 mm Hg?

 

Solution :

 

 According to the question, V₁ = 400 cm³

T₁ = 0^oC = 0 + 273 = 273K

T₂ = 80^oC = 80 + 273 = 353K

You need to find the V₂.

Here, only the temperature is changing, the pressure remains constant

Using Charle’s law, V₁/T₁ = V₂/T₂

Putting the above values in Charle’s law, we get,

400/273 = V₂/353

V₂ = 400 x 353/273

V₂ = 517.21 cm³

Since 1 cubic centimetres = 0.001 litres,

517.21 cubic centimetres = 517.21 x 10^-3 = 0.517 litres.

 

 

2.    A sample of gas has an initial volume of 30.8 L and an initial temperature of -67^oC. What will be the temperature of the gas if the volume is 21.0 L?

 

Solution :

 

According to the question,

V₁ = 30.8L

T₁ = – 67 degree celsius = 206 K

T₂ = ?

V₂ = 21.0L

 

According to Charle’s law,

V₁/T₁ = V₂/T₂

30.8/67 = 21/T2

T₂ = 21 x 67/30.8

= 46.9°C

 

If V₁ is the 3.60 L, T₁ = 255 K , T₂ = 102K , then find the value of V₂.

According to the question V₂ =?

As we are aware of Charle’s law,

V₁/T₁ = V₂/T₂

3.6/255 = V₂/102

V₂ = 1.44 L

 

3.    A gas occupies 221 cm³ at a temperature of 0^oC and pressure of 760 mm Hg. What will be the volume at 100^oC.

 

 

Solution :

 

It is very clear that the pressure is constant, and the mass of the gas doesn’t change, so we can apply Charle’s law here.

The temperature in the question is given in Celcius, so as per the rule of Charle’s law, it must be converted to the absolute temperature, that is, Kelvin, to apply the formula :

V₁ = 221 cm³ , T₁ = (0 + 273) = 273 K , T₂ = (100 + 273) = 373 K

Now, these given values can be put in the formula to get the final volume.

V_I/T_I = V_F/T_F

221/273 = V_F/373

By rearranging the above equation, we will get the final volume

V_F = (221) x (373)/273 K

V_F = 302 cm³

 

 

 

Gay-Lussac’s Law

 

Propane tanks are extensively used in the kitchen. It’s not enjoyable, however, to discover you’ve run out of gas halfway through a meal. On a hot day, gauges are used to measure the pressure inside gas tanks that read greater than on a cool day. When deciding whether or not to replace the tank before your next cookout, keep the air temperature in mind. In this article, we’ll go over Gay Lussac’s Law in detail, including its formula and derivation.

          Gay-Lussac’s law is a gas law which states that the pressure exerted by a gas (of a given mass and kept at a constant volume) varies directly with the absolute temperature of the gas. In other words, the pressure exerted by a gas is proportional to the temperature of the gas when the mass is fixed and the volume is constant.

          This law was formulated by the French chemist Joseph Gay-Lussac in the year 1808. The mathematical expression of Gay-Lussac’s law can be written as follows :

 

 

 

P∝ T

 

Or,  P/T = k

 

Where :

·       P is the pressure exerted by the gas

·       T is the absolute temperature of the gas

·       k is a constant

 

The relationship between the pressure and absolute temperature of a given mass of gas (at constant volume) can be illustrated graphically as follows.

                                   

 

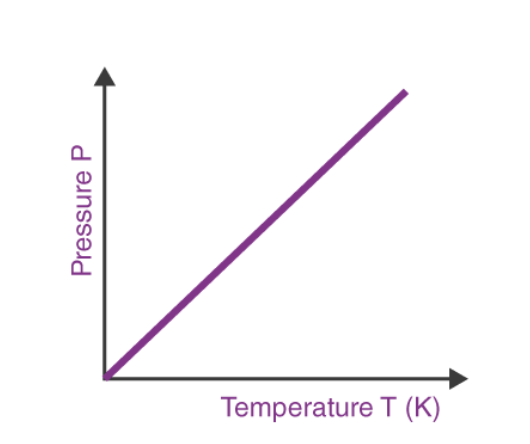
From the graph, it can be understood that the pressure of a gas (kept at constant volume) reduces constantly as it is cooled until the gas eventually undergoes condensation and becomes a liquid.

 

 

Formula and Derivation

Gay-Lussac’s law implies that the ratio of the initial pressure and temperature is equal to the ratio of the final pressure and temperature for a gas of a fixed mass kept at a constant volume. This formula can be expressed as follows:

                                               (P₁/T₁) = (P₂/T₂)

Where :

·       P₁ is the initial pressure

·       T₁ is the initial temperature

·       P₂ is the final pressure

·       T₂ is the final temperature

 

This expression can be derived from the pressure-temperature proportionality for gas. Since P & T for gases of fixed mass kept at constant volume:

P₁/T₁= k (initial pressure/ initial temperature = constant)

P₂/T₂ = k (final pressure/ final temperature = constant)

Therefore,    P₁/T₁ = P₂/T₂ = k

Or,                P₁T₂ = P₂T₁

Examples of Gay-Lussac’s Law

 

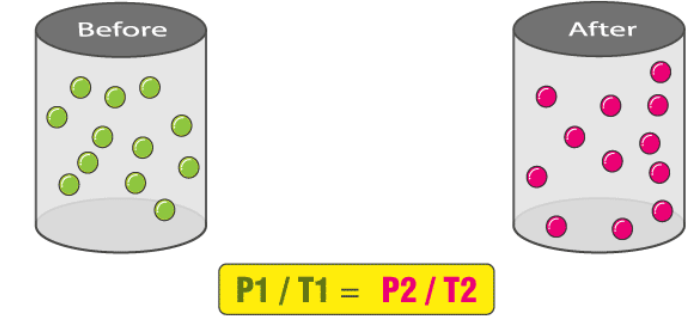
When a pressurized aerosol can (such as a deodorant can or a spray- paint can) is heated, the resulting increase in the pressure exerted by the gases on the container (owing to Gay-Lussac’s law) can result in an explosion. This is the reason why many pressurized containers have warning labels stating that the container must be kept away from fire and stored in a cool environment.

 

An illustration describing the increase in pressure which accompanies an increase in the absolute temperature of a gas kept at a constant volume is provided above. Another example of Gay-Lussac’s law can be observed in pressure cookers. When the cooker is heated, the pressure exerted by the steam inside the container increases. The high temperature and pressure inside the container cause the food to cook faster.

 

 

Solved Exercises on Gay-Lussac’s Law

Exercise 1

The pressure of a gas in a cylinder when it is heated to a temperature of 250 K is 1.5 atm. What was the initial temperature of the gas if its initial pressure was 1 atm?

 

Solution :

 

Given,

Initial pressure, P₁ = 1atm

Final pressure, P₂ = 1.5 atm

Final temperature, T₂ = 250 K

As per Gay-Lussac’s Law, P₁T₂ = P₂T₁

Therefore, T₁ = (P₁T₂)/P₂ = (1 x 250)/(1.5) = 166.66 Kelvin.

  

Exercise 2

At a temperature of 300 K, the pressure of the gas in a deodorant can is 3 atm. Calculate the pressure of the gas when it is heated to 900 Κ.

 

Solution :

 

Initial pressure, P₁ = 3 atm

Initial temperature, T₁ = 300 K

Final temperature, T₂ = 900 K

Therefore, final pressure (P₂) = (P₁T₂)/T₁

                                                = (3 atm x 900 K)/300 K = 9 atm.

 

Combined Gas Law

 

The combined gas law is the law which combines Charles’s law, Gay- Lussac’s law and Boyle’s law. It’s an amalgamation of the three previously discovered laws. These laws relate one thermodynamic variable to another holding everything else constant. The interdependence of these variables represents combined gas law which states that the ratio between the product of pressure-volume and temperature of a system remains constant.

 

Combined Gas Law Formula

Combined gas law can be mathematically expressed as,

PV/T = K

Where,

P = pressure

T = temperature in kelvin

V = volume

K = constant (units of energy divided by temperature)

 

When two substances are compared in two different conditions, the law can be stated as,

 

                                                P_iV_i/T_i = P_fV_f/T_f

Where,

P_i = initial pressure

V_i = initial volume

T_i = initial temperature

P_f = final pressure

V_f = final volume

T_f = final temperature

 

 

Solved Exercises on Combined Gas Law

 

Example 1

The initial volume of the gas is 5 L and final volume is 3 L Calculate the final pressure of the gas, given that the initial temperature is 273 K, the final temperature is 200 K, and initial pressure is 25 kPa.

 

Solution :

 

According to the given parameters,

P_i = 25 kPa

V_i = 5 L

V_f = 3 L

T_i = 273K

T_f = 200K

 

According to combined gas law,

P_iV_i/T_i = P_fV_f/T_f

 

Substituting in the formula, we get

(25 x 5)/273 = (P_f x 3)/200

Therefore, P_f = 30.525 kPa

 

Example 2

Determine the volume of a gas given V_i = 3 L T_i = 300 K T_f = 250K, P_i = 35 kPa and P_f = 50 kPa.

 

Solution :

 

Given Parameters are,

Pi = 35 kPa

Vi = 3L

Ti = 300K

P_f = 50 kPa

T_f = 250K

 

According to given parameters, we have an equation,

P_iV_i/T_i = P_fV_f/T_f

 

Substituting in the above equation,

we get,

(35 x 3)/300 = (50 x V_f)/250

Therefore, V_f = 1.75 L

 

 

 

 Ideal Gas Law

 

The ideal gas law, also known as the general gas equation, is an equation of the state of a hypothetical ideal gas. Although the ideal gas law has several limitations, it is a good approximation of the behavior of many gases under many conditions. Benoit Paul Émile Clapeyron stated the ideal gas law in 1834 as a combination of the empirical Charles’s law, Boyle’s Law, Avogadro’s law, and Gay- Lussac’s law.

The ideal gas law states that the product of the pressure and the volume of one gram molecule of an ideal gas is equal to the product of the absolute temperature of the gas and the universal gas constant.

 

The empirical form of ideal gas law is given by :

   PV = nRT 

where,

P is the pressure.

V is the volume.

n is the amount of substance.

R is the ideal gas constant.

T is the absolute temperature of the gas.

 

Ideal Gas Law Units

·       When we use the gas constant R = 8.31 J/K.mol, then we have to plug in the pressure P in the units of pascals Pa, volume in the units of m³ and the temperature T in the units of kelvin K.

 

·       When we use the gas constant R = 0.082 L.atm/K.mol then pressure should be in the units of atmospheres atm, volume in the units of litres L and the temperature T in the units of kelvin K.

For easy reference, the above information is summarized in the table as follows :

 

 

Ideal Gas Equation Units
R = 8.314 J/K.mol	R = 0.082 L.atm/K.mol
Pressure in pascals, Pa	Pressure in atmosphere, atm
Volume in m3	Volume in litres L
The temperature in Kelvin K	The temperature in Kelvin K

 

 

 

 

 

 

 

Derivation of the Ideal Gas Law

The ideal gas law is derived from the observational work of Robert Boyle, Gay-Lussac and Amedeo Avogadro. Combining their observations into a single expression, we arrive at the Ideal gas equation, which describes all the relationships simultaneously.

The three individual expressions are as follows :

 

Boyle’s Law

V ∝  1/P

 

Charle’s Law

V ∝  T

 

Avogadro’s Law

V ∝  n

 

Combining these three expressions, we get

V ∝  nT/P

The above equation shows that volume is proportional to the number of moles and the temperature while inversely proportional to the pressure.

This expression can be rewritten as follows :

 

V = RnT =  nRT

        P         P

 

Multiplying both sides of the equation by P to clear off the fraction, we get,

 

  PV = nRT

 

The above equation is known as the ideal gas equation.

 

 

Ideal Gas Law Solved Problems

 

1.    What is the volume occupied by 2.34 grams of carbon dioxide gas at STP?

 

Solution :

 

To determine the volume, rearrange the ideal gas law as follows:

V = nRT/P

Substituting the values as follows, we get

V = [(2.34g / 44g.mol^-1) (0.08206 L atm mol^-1 K^-1) (273.0K)] / 1.00 atm 

V = 1.19 L

 

 

2.    Calculate the temperature at which 0.654 moles of neon gas occupies 12.30 litres at 1.95 atmospheres.

 

Solution :

 

To determine the temperature, rearrange the ideal gas equation as follows:

T = PV/nR

Substituting the value, we get

 T = (1.95 atm)) (12.30L) / (0.654 mol) (0.08206 L atm mol-¹K-1) 

 T = 447 K

 

Relationship between Pressure and Temperature

The graph here shows the relationship between temperature and pressure for different gases.

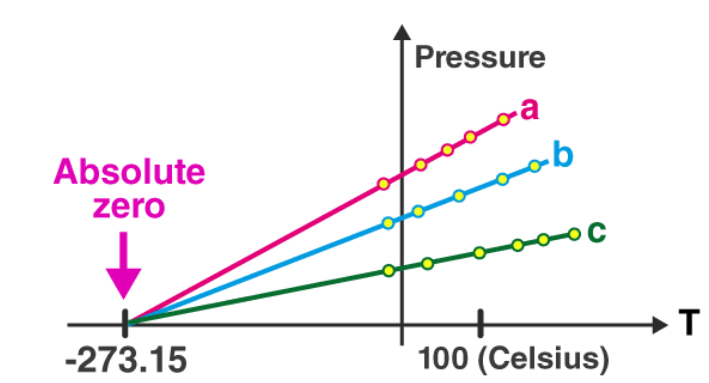
On extrapolating this graph, we see that the graphs always intercept the x-axis at a point we now call the absolute zero, irrespective of which gas we are graphing. This point represents the beginning of the Kelvin scale, i.e. Zero K. On the Celsius scale, 0 K is equivalent to -273.5 °C. This is the coldest temperature possible. As a molecule gets colder, its energy and, consequently, its movement and vibrations decrease in amplitude. As we keep cooling it, at a point, the atom will reach a state of minimum  internal energy where the atom has lost almost all its energy and is stationary.

The gas constant and the units of the ideal gas equation

R is called the gas constant and it has a value of 8.31 J K^–¹ mol^–¹. This value is provided in section 2 of the Data booklet.

The inclusion of R in the ideal gas equation requires the following units : P (Pa), V (m³), and T (K).

Note that, 1 Pa = 1J m^-3 , this allows you to see how the units in the ideal gas equation are balanced:

P(J m^–³) × V(m³) = n(mol) × R(JK^–¹ mol^–¹) x T(K)

1 dm³ = 1 x 10^-3 m³

 

 

 Avogadro’s Law

 

Avogadro’s law, also known as Avogadro’s principle or Avogadro’s hypothesis, is a gas law which states that the total number of atoms/molecules of a gas (i.e. the amount of gaseous substance) is directly proportional to the volume occupied by the gas at constant temperature and pressure.

 

Avogadro’s law is closely related to the ideal gas equation since it links temperature, pressure, volume, and amount of substance for a given gas.

 

Avogadro’s law is named after the Italian scientist Amedeo Carlo Avogadro, who suggested that two dissimilar ideal gases occupying the same volume at a given (constant) temperature and pressure must contain an equal number of molecules.

 

Formula and Graphical Representation

At constant pressure and temperature, Avogadro’s law can be expressed via the following formula:

V ∝ n

 

 

 

V/n = k

 

Where V is the volume of the gas, n denotes the amount of gaseous substance (often expressed in moles), and k is a constant. When the amount of gaseous substance is increased, the corresponding increase in the volume occupied by the gas can be calculated with the help of the following formula : 

 

 

  V₁/n₁ = V₂/n₂     (= k, as per Avogadro’s law).

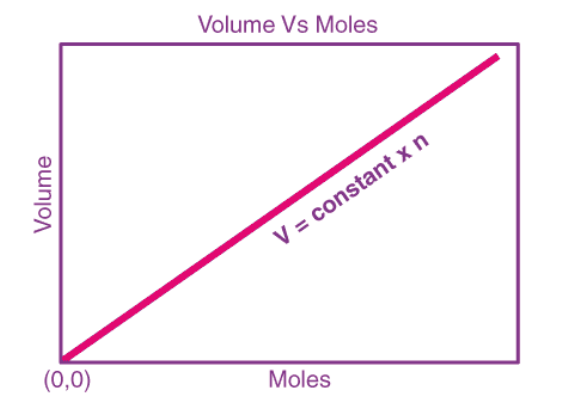
The graphical representation of Avogadro’s law (with the amount of substance on the X-axis and volume on the Y-axis) is illustrated below.

Here, the straight line (which indicates that the two quantities are directly proportional) passes through the origin, implying that zero moles of gas will occupy zero volume.

 

Derivation

Avogadro’s law can be derived from the ideal gas equation, which can be expressed as follows:

PV = nRT

Where,

·       ‘P’ is the pressure exerted by the gas on the walls of its container

·       ‘V’ is the volume occupied by the gas

·       ‘n’ is the amount of gaseous substance (number of moles of gas)

·       ‘R’ is the universal gas constant

·       ‘T’ is the absolute temperature of the gas

 

Rearranging the ideal gas equation, the following equation can be obtained.

V/n = (RT)/P

Here, the value of (RT)/P is a constant (since the temperature and pressure kept constant and the product/quotient of two or more constants is always a constant). Therefore :

V/n = k

Thus, the proportionality between the volume occupied by a gas and the number of gaseous molecules is verified.

Molar Volume of a Gas

As per Avogadro’s law, the ratio of volume and amount of gaseous substance is a constant (at constant pressure and temperature). The value of this constant (k) can be determined with the help of the following equation :

k = (RT)/P

Under standard conditions for temperature and pressure, the value of T corresponds to 273.15 Kelvin and the value of P corresponds to 101.325 kilo Pascals. Therefore, the volume occupied by one mole of a gas at STP is :

Volume occupied by 1 mole of gas = (8.314 J.mol^–¹.K^–¹)x(273.15 K)/ (101.325 kPa) = 22.4 litres

Therefore, one mole of any gaseous substance occupies 22.4 litres of volume at STP.

 

Examples of Avogadro’s Law

The process of respiration is a great example of Avogadro’s law. When humans inhale, the increase in the molar quantity of air in the lungs is accompanied by an increase in the volume of the lungs (expansion of the lungs). An image detailing the change in volume brought on by an increase in the number of gaseous molecules is provided below.

 

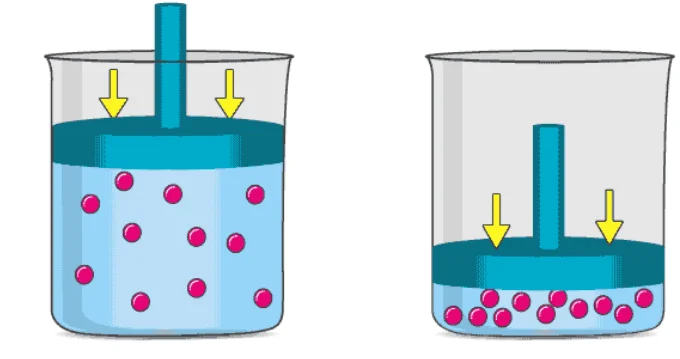
Another common example of Avogadro’s law is the deflation of automobile tyres. When the air trapped inside the tyre escapes, the number of moles of air present in the tyre decreases. This results in a decrease in the volume occupied by the gas, causing the tyre to lose its shape and deflate.

 

What are the Limitations of Avogadro’s Law?

Despite being perfectly applicable to ideal gases, Avogadro’s law provides only approximate relationships for real gases. The deviation of real gases from ideal behavior increases at low pressure and high temperature.

It is important to note that gases molecules having relatively low molecular masses (such as helium and hydrogen) obey Avogadro’s law to a greater extent than heavier molecules.

 

 

Solved Exercises on Avogadro’s Law

 

Example 1

One mole of helium gas fills up an empty balloon to a volume of 1.5 litres. What would be the volume of the balloon if an additional 2.5 moles of helium gas is added? (Assume that the temperature and the pressure are kept constant)

 

Solution :

 

Given,

The initial amount of helium (n₁) = 1 mol

The initial volume of the balloon (V₁) = 1.5 L

The final amount of helium (n₂) = 1 mol + 2.5 mol = 3.5 mol

As per Avogadro’s law, V₁/n₁ = V₂/n₂

Therefore, the final volume of the balloon,

 V₂ = (V₁n₂) / n₁ = (1.5 L x 3.5 mol) / 1mol = 5.25 L

The balloon would occupy a volume of 5.25 litres when it contains 3.5 moles of helium gas.